Geometria este una dintre ramurile cele mai fascinante ale matematicii, având aplicații practice în aproape toate aspectele vieții noastre – de la arhitectură și inginerie, până la design și tehnologie. Una dintre primele figuri geometrice pe care le studiem încă din clasele primare este triunghiul, un poligon cu trei laturi și, implicit, cu trei unghiuri. Înțelegerea modului în care putem calcula unghiurile unui triunghi este esențială, nu doar pentru a trece cu bine de teme și examene, ci și pentru a dezvolta raționamentul logic și gândirea spațială.
În acest articol, vom explora în detaliu cum se calculează unghiurile unui triunghi, vom analiza regulile de bază, vom rezolva exemple practice și vom discuta despre tipurile de triunghiuri și cum influențează acestea valorile unghiurilor. Vom explica totul pas cu pas, într-un mod clar și accesibil, indiferent dacă ești elev, părinte sau doar persoană curioasă să-și reîmprospăteze cunoștințele de geometrie.
🔺 Ce este un triunghi?
Înainte de a ne apuca de calcule, să ne întoarcem puțin la baze: ce este, de fapt, un triunghi?
Un triunghi este o figură geometrică închisă, formată din trei segmente de dreaptă (numite laturi) care se întâlnesc două câte două în trei puncte distincte, numite vârfuri. La fiecare vârf se formează un unghi, deci orice triunghi are trei unghiuri interioare.
Unghiurile interioare ale unui triunghi sunt notate de obicei cu litere grecești precum α (alfa), β (beta) și γ (gamma), sau prin notația vârfurilor, cum ar fi ∠A, ∠B, ∠C.
⚖️ Regula de bază: Suma unghiurilor unui triunghi este întotdeauna 180 de grade
Una dintre cele mai importante proprietăți ale triunghiurilor este următoarea:
Suma măsurilor unghiurilor interioare ale oricărui triunghi este egală cu 180 de grade.
Această regulă este universal valabilă, indiferent de tipul triunghiului – fie că este isoscel, echilateral, dreptunghic sau oarecare. Este o consecință directă a axiomaticii geometriei euclidiene și a fost demonstrată încă din antichitate.
Această regulă este cheia pentru a determina măsura unui unghi necunoscut atunci când cunoaștem valorile altor două unghiuri.
🔢 Cum se calculează un unghi necunoscut al unui triunghi?
Să presupunem că avem un triunghi în care cunoaștem măsurile a două dintre unghiurile sale. Cum aflăm valoarea celui de-al treilea unghi?
✅ Pașii pentru calcul:
- Măsoară sau identifică două unghiuri ale triunghiului.
- Adună cele două unghiuri cunoscute.
- Scade suma obținută din 180°.
- Rezultatul este măsura unghiului necunoscut.
Să vedem cum funcționează acest proces în practică.
📘 Exemplu 1: Caz concret de calcul
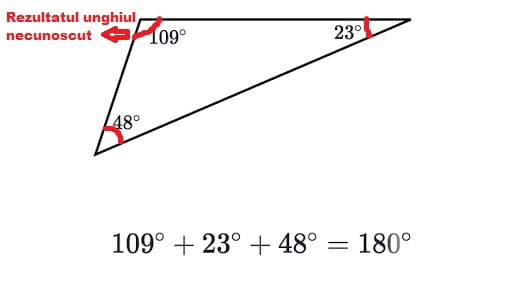
Avem un triunghi în care două dintre unghiuri măsoară 48° și 23°. Care este măsura celui de-al treilea unghi?
- Adunăm unghiurile cunoscute:
( 48° + 23° = 71° ) - Scădem din 180°:
( 180° – 71° = 109° )
➡️ Așadar, cel de-al treilea unghi măsoară 109°.
Această valoare pare mare? Poate părea, dar este perfect posibilă. Triunghiul nostru are un unghi obtuz (mai mare de 90°), ceea ce îl face un triunghi obtuzunghic. Totul este în regulă cu regula sumei de 180°.
📘 Exemplu 2: Un alt caz simplu
Să luăm un alt exemplu: un triunghi cu unghiurile de 105° și 35°.
- Adunăm valorile cunoscute:
( 105° + 35° = 140° ) - Scădem din 180°:
( 180° – 140° = 40° )
➡️ Al treilea unghi măsoară 40°.
Verificăm: ( 105° + 35° + 40° = 180° ) – corect!
❗ De reținut: Suma unghiurilor = 180°
Această regulă este atât de importantă încât merită scrisă mare și colorată:
Suma tuturor unghiurilor interioare ale unui triunghi este întotdeauna 180°.
Dacă, la verificare, suma dă un rezultat diferit (de exemplu, 170° sau 190°), atunci fie ați făcut o greșeală în calcule, fie măsurătorile inițiale sunt incorecte.
🛠️ Cum măsurăm unghiurile unui triunghi?
Înainte să putem face adunări și scăderi, trebuie să știm cum măsurăm unghiurile. Instrumentul cel mai folosit este raportorul.
Pașii pentru măsurarea unui unghi cu raportorul:
- Plasați centrul raportorului (de obicei marcat printr-o cruce sau un cerc) pe vârful unghiului.
- Aliniați una dintre laturile unghiului cu linia de 0° a raportorului.
- Citiți valoarea de pe raportor care corespunde celei de-a doua laturi a unghiului.
- Notați măsura în grade.
În cazul triunghiurilor desenate sau prezentate pe hârtie sau pe ecran, raportorul digital sau instrumentele CAD (proiectare asistată de calculator) pot fi de mare ajutor.
🔍 Tipuri de triunghiuri și impactul asupra unghiurilor
Triunghiurile nu sunt toate la fel. Ele pot fi clasificate în funcție de lungimile laturilor sau de natura unghiurilor. Fiecare tip are caracteristici specifice care influențează unghiurile.
1. Triunghi echilateral
- Toate laturile sunt egale.
- Toate unghiurile sunt egale.
- Fiecare unghi măsoară: ( 180°:3 = 60° )
👉 Exemplu: dacă știi că un triunghi este echilateral, nu ai nevoie să măsori unghiurile – toate sunt de 60°.
2. Triunghi isoscel
- Doar două laturi sunt egale.
- Cele două unghiuri opuse laturilor egale sunt întotdeauna egale între ele.
👉 Exemplu: dacă un triunghi isoscel are un unghi de bază de 50°, atunci celălalt unghi de bază este tot de 50°, iar unghiul de la vârf va fi:
( 180° – (50° + 50°) = 80° )
3. Triunghi scalen
- Toate laturile și unghiurile sunt diferite.
- Nu există reguli automate – fiecare unghi trebuie măsurat sau calculat individual.
4. Triunghi dreptunghic
- Un unghi este întotdeauna de 90° (unghi drept).
- Celelalte două unghiuri sunt ascuțite (mai mici de 90°) și se numesc complementare, pentru că suma lor este ( 90° ).
👉 Exemplu: dacă un unghi al unui triunghi dreptunghic este de 35°, atunci celălalt unghi ascuțit este:
( 90° – 35° = 55° )
Și verificăm: ( 35° + 55° + 90° = 180° ) – corect!
✅ Cazuri speciale: Când nu cunoști niciun unghi?
În unele situații, poți avea informații despre laturile triunghiului, fără să știi nimic despre unghiuri. În acest caz, poți folosi teorema cosinusului sau teorema sinusurilor pentru a determina unghiurile.
De exemplu, dacă cunoști toate cele trei laturi ale unui triunghi, poți aplica:
- Legea Sinusurilor: Raportul dintre lungimea unei laturi și sinusul unghiului opus este constant pentru toate laturile triunghiului.
a / sin(A) = b / sin(B) = c / sin(C) = 2R(unde R este raza cercului circumscris triunghiului).
- Aplicație: Dacă cunoaștem o latură și unghiul opus ei, precum și o altă latură, puteți calcula sinusul unghiului opus acesteia și, implicit, unghiul.
- Legea Cosinusurilor: Este o generalizare a teoremei lui Pitagora pentru triunghiuri oarecare.
c² = a² + b² - 2ab * cos(C)
- Aplicație: Poate fi utilizată pentru a găsi:
- O latură când se cunosc celelalte două laturi și unghiul dintre ele.
- Un unghi când se cunosc toate cele trei laturi (prin rearrangarea formulei:
cos(C) = (a² + b² - c²) / (2ab)).
Aceeste se învață de obicei în liceu, dar sunt metode foarte eficientă pentru triunghiuri oarecare.
Totuși, pentru nivelul gimnazial sau pentru calcule rapide, regula celor 180 de grade rămâne cea mai simplă și utilă.
🧠 Sfaturi pentru o înțelegere mai bună
- Desenează mereu figurile – O schiță clară ajută la vizualizarea datelor și a cerințelor.
- Etichetează unghiurile – Notează-le cu valori sau simboluri pentru a evita confuzia.
- Folosește hârtie cu pătrățele – Ajută la desenarea mai precisă a triunghiurilor.
- Verifică întotdeauna suma totală – Dacă nu dă 180°, revino asupra calculelor.
- Exersează cu diverse tipuri de triunghiuri – Cu cât vezi mai multe cazuri, cu atât devii mai sigur în abilitățile tale.
💡 Aplicații practice ale cunoașterii unghiurilor triunghiului
Calculul unghiurilor nu este doar un exercițiu școlar. Are aplicații reale în multe domenii:
- Arhitectură: pentru proiectarea acoperișurilor, scărilor sau structurilor stabile.
- Navigație: în determinarea direcțiilor folosind triangulație.
- Inginerie: în calculul forțelor și tensiunilor în structuri metalice.
- Design grafic: pentru alinierea corectă a elementelor în spațiu.
- Jocuri video: în programarea mișcării și coliziunilor obiectelor.
❓ Întrebări frecvente (FAQ)
Q: Poate avea un triunghi un unghi de 180°?
R: Nu. Dacă un unghi ar fi de 180°, celelalte două ar trebui să fie de 0°, ceea ce ar însemna că triunghiul “se prăbușește” într-o linie dreaptă. Nu mai este un triunghi.
Q: Poate un triunghi avea două unghiuri drepte?
R: Nu. Dacă ar avea două unghiuri de 90°, suma lor ar fi deja 180°, iar al treilea unghi ar trebui să fie 0° – imposibil.
Q: Ce se întâmplă dacă suma unghiurilor dă mai mult de 180°?
R: În geometria euclidiană (cea studiată în școală), acest lucru nu se poate întâmpla. Dacă se întâmplă, înseamnă că s-a greșit undeva – fie la măsurare, fie la calcul.
✍️ Concluzie: Geometria e simplă când înțelegi regulile
Calculul unghiurilor unui triunghi este o operație simplă dacă ții minte o singură regulă: suma unghiurilor interioare este 180°. Cu această bază solidă, orice problemă devine accesibilă. Fie că ai de găsit un unghi necunoscut, fie că trebuie să verifici dacă un triunghi este bine construit, toate se reduc la adunări și scăderi simple.
Înțelegerea triunghiurilor este primul pas către o cunoaștere mai profundă a geometriei. Îți dezvoltă gândirea critică, simțul spațial și abilitatea de a rezolva probleme în lumea reală.
Așadar, data viitoare când vei vedea un triunghi – fie pe o foaie de matematică, fie în forma unui acoperiș sau a unui panou indicativ – oprește-te o secundă și gândește-te: „Ce unghiuri are? Ce tip de triunghi e? Și, mai important, cum pot calcula ce nu știu?”
Geometria este peste tot în jurul nostru. Iar tu, acum, ai instrumentele pentru a o înțelege.
📚 Materiale recomandate pentru antrenament
Dacă vrei să exersezi mai mult, iată câteva tipuri de exerciții:
- Dă 5 exemple de triunghiuri isoscele și calculează unghiurile necunoscute.
- Desenează un triunghi dreptunghic și calculează unghiurile cunoscând doar unul dintre cele ascuțite.
- Construiește un triunghi echilateral și măsoară unghiurile cu raportorul – vei vedea că sunt exact 60°.
- Creează un triunghi obtuzunghic și verifică că suma unghiurilor rămâne 180°.
„Matematica este regina științelor, iar geometria este regina matematicii.” – Carl Friedrich Gauss
Așadar, fiecare pas pe care îl faci în înțelegerea geometriei te apropie de o lume mai ordonată, mai logică și mai frumoasă. Și totul începe cu un simplu triunghi.